Zitat:
Zitat von zeitgenosse

Erkläre mir doch einfach kurz und bündig, um was es sich bei der Einstein-Lobatschewski-Geometrie des "Geschwindigkeitsraums" handelt.
|
Typisch für SCR - er schweigt, wenn er überfordert ist!
Ich übernehme deshalb gerne die Antwort. Zunächst mit einem Eingeständnis:
Der Ausdruck "Einstein-Lobatschewski-Geometrie" war mir bisher nicht geläufig.
Weder
Schröder (Spezielle Relativitätstheorie, Verlag Harri Deutsch)
noch
Freund (Spezielle Relativitätstheorie für Studienanfänger, vdf Hochschulverlag)
noch
Günther (Spezielle Relativitätstheorie, Teubner)
führen diesen Terminus in ihrem Repertoir; doch das hat nichts zu sagen.
Inzwischen weiss ich trotzdem, was das von SCR angesprochene Physiklexikon unter einer Einstein-Lobatschewski-Geometrie versteht; doch m.E. ist dieser Begriff unglücklich gewählt. Denn die Riemannsche und die Lobatschewski'sche Geometrie schliessen sich aufgrund ihrer verschiedenartigen Krümmung gegenseitig aus. Im Gesamtgebäude der Geometrie sind natürlich beide dieser nichteuklidischen Geometrien gleichberechtigt. Besser in meinen Augen wäre infolgedessen die Begrifflichkeit "Lorentz-Geometrie der Raumzeit".
Um was geht es im Kontext:
Geschwindigkeiten sollen relativistisch zueinander in eine Relation gesetzt werden.
Mit c=1 gilt in einem Raumzeit-Diagramm in der Minkowski-Ebene:
u = (w - v)/(1 - wv)
v Geschwindigkeit von Inertialsystem K
w Geschwindigkeit von Inertialsystem K'
Als u wird hier die Relativgeschwindigkeit zwischen zwei Inertialsystemen bezeichnet, also z.B. diejenige Geschwindigkeit, mit der ein antriebsloses Raumschiff ein zweites ebensolches überholt (solange dabei die Gravitation vernachlässigbar ist).
Verwenden wir als elementares Beispiel zwei Inertialsysteme K und K', wobei K als ruhend (Weltlinie entlang der ct-Achse) angenommen wird. Das zweite System K' werde zur Zeit t = 0 von K ausgestossen und bewege sich mit gleichförmiger Geschwindigkeit durch den Raum. Betrachtet man nun die Weltlinien beider Systeme, so wird ersichtlich, dass die Relativgeschwindigkeit durch den Tangens des von beiden Weltlinien eingeschlossenen Winkels festgelegt wird.
Ersetzt man in einem weiteren Schritt die Geschwindigkeiten (u,v,w) durch den zugehörigen 'Tangens hyperbolicus' (eine Hyperbelfunktion), so ergibt sich:
v = tanh α
w = tanh β
u = tanh γ
Allgemein gilt:
tanh(x) := sinh(x)/cosh(x)
http://upload.wikimedia.org/wikipedi..._cosh_tanh.svg
Das Einsteinsche Geschwindigkeitstheorem nimmt damit eine besonders einfache Form an:
γ = β - α
Aus der Hyperbelfunktion f(x) = tanh erkennt man zudem unschwer, dass eine Grenzgeschwindigkeit (c=1) nicht überschritten werden kann:
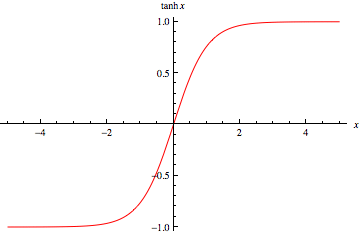
Dass hier anstelle des ansonsten üblichen tan der weniger bekannte tanh Verwendung findet, folgt aus der Verschiedenheit der euklidischen und Lorentz'schen Geometrie. Ist in der euklidischen Ebene der Einheitskreis die Eichfunktion, so ist es in der Minkowski-Ebene die Einheitshyperbel:
x² - y² = cosh²[A] - sinh²[A] = 1
p.s.
Der Ausdruck Einstein-Lobatschewski-Geometrie entspringt aufgrund des Gesagten vermutlich dem Umstand, dass im Geschwindigkeitsraum (besser wäre im Minkowskiraum) eine hyperbolische Funktion zur Anwendung kommt. Ungeachtet dessen - und um Verwechslungen zu vermeiden - verwende ich lieber den bekannteren Ausdruck "Lorentz-Geometrie".
Eine Einführung in die Lorentz-Geometrie ist bspw. enthalten bei:
Knörrer, Geometrie (Vieweg+Teubner)
Gr. zg