*************************
Schwingungs (harmonische) DZGL
*************************
x[1]:=cos(dx); dx ist die Schrittweite
y[1]:=sin(dx);
x[n+1]:=x[n]*c1 - y[n]*c2; # -> Cosinuswerte
y[n+1]:=y[n]*c1 + x[n]*c2; # -> Sinuswerte
Herleitung :
Eine exakte ! numerische Simulation der harmonischen Schwingung ergbt sich aus den Additionstheoremen.
Additionstheoreme
**************
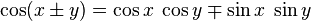

Fuer eine Startwert x und eine Schrittweite dx erhaelt man aus der ersten Gleichung:
cos(x+dx)=cos(x)*cos(dx)-sin(dx)*sin(x)
Anm: Ziel ist es eine Substitution X(n)=cos(x+n*dx) durchzufuehren.
Die Werte fuer die Sinusfunktion koennte man ueber die Beziehung sin(x)^2+cos(x)^2=1 ausdruecken. Allerdings weist eine solche lteration aufgrund des Wurzelvorzeichens lediglich enen Gueltigkeitsbereich im Intervall 0-180 Grad auf :

Eleganter,allgemeiner und effizienter ist es die Sinusfunktion ebenfalls iterativ aus dem Additionstheorem zu berechnen :
cos(x+dx)=cos(x)*cos(dx)-sin(dx)*sin(x)
sin(x+dx)=sin(x)*cos(dx)+sin(dx)*cos(x)
dx stellt in einer iterativen Betrachtung eine Konstante dar =>
cos(x+dx)=c1*cos(x)-c2*sin(x)
sin(x+dx)=c1*sin(x)+c2*cos(x)
die Gleichungen sind exakt fuer :
c1=cos(dx)
c2=sin(dx)
Erstetz man C1 ud C2 durch Taylorapproximationen erhaelt man 1.Ordnung eine Variante der Euler Chromer Integration. (Nur eine formale Variante !)
c1=1
c2=0
Die "Merman Naeherung" entspricht eine Taylorapproximation 2.Ordung die sich auch graphisch herleiten laesst.
c1:=1-dx^2/2;
c2:=sqrt(dx^2-dx^4/4);
(Notwendig sind solche Approximationen nicht.)
Mittels Substitution erhalten wir ein DZL System fuer X(n),Y(n)
(Im folgenden in Kleinbuchstaben geschrieben)
Zitat:
|
Zitat von Quellcode
restart;
N:=360; # Anzahl Abtastwerte
P:=3; # Anzahl Perioden
M:=P*N;
dx:=evalf(2*Pi/N);
c1:=1-dx^2/2; #(Beispiel Menrman Naeherung)
c2:=sqrt(dx^2-dx^4/4); #(Beispiel Menrman Naeherung)
x[1]:=c1;
y[1]:=c2;
for n from 1 to M do
x[n+1]:=x[n]*c1 - y[n]*c2; # -> Cosinuswerte
y[n+1]:=y[n]*c1 + x[n]*c2; # -> Sinuswerte
od:
# DRUCKROUTINEN
druck1:=seq([i,y[i]],i=1..M):
druck2:=seq([i,sin(i*2*Pi/360)],i=1..M):
druck3:=seq([i,x[i]],i=1..M):
druck4:=seq([i,cos(i*2*Pi/360)],i=1..M):
plot([[druck1],[druck2],[druck3],[druck4]]);
|
Der Cordic Algo baut auf die vorgestellte DZGL auf.
Die Taylor (graphischen) Naeherungen sind nur von theoretischen Interesse, da die Methode der Additionstheoreme exakt ist. Diese stellt keine integrale Appproximation dar ! Bereits eine Taylor, Merman Approximation 2.ter Ordnung ist sehr genau.

Da die Approximation nach den Additionstheoremen exakt ist, stellt die Loesung der DZGL die harmonische Schwingung dar. Die Taylor Naeherungen ergeben dagegen sehr komplexe Ausdruecke fuer die Loesung.
(Kommentare bitte im Diskussionsthread :-)