Hi Merman
Zitat:
Zitat von Lutzl, zu meiner Herleitung (Wiki-Mathematiker):
„Je genauer dieses Vorgehen wird, desto mehr Rechenschritte und desto mehr Rundungsfehler akkumulieren sich. Deshalb ist Halbieren und Quadrieren besser, aber ebenfalls zu langsam.“
|
Seltsamer Mathematiker. Pauschal gesehen stimmt diese Aussage ueberhaupt nicht.
Wie waere es, wenn wir einfach mal die Iteration herleiten, die sich aus dem Additionstheorem ergibt und dann vergleichen ?
Deine Approximation lautet :
m0:=evalf(Pi/180);
c1:=1-m0^2/2;
c2:=sqrt(m0^2-m0^4/4);
x[1]:=c1;
for n from 1 to 360 do
x[n+1]:=x[n]*c1 - sqrt(1-x[n]^2)*c2;
y[n+1]:=sqrt(1-x[n+1]^2); # -> Sinuswerte
od;
Das Additionstheorem
****************
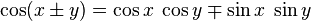

Du berechnest den Kosinus und dies entspricht der ersten Gleichung :
1) cos(x+y)=cos(x)*cos(y)-sin(y)*sin(x)
(Mittels der zweiten Gleichung haettest du dir die Umrechnung nach Sinus sparen koennen)
Setzten wir einfach mal in der Gleichung fuer x ein festes x0 und fuer y eine Abweichung dx davon :
cos(x0+dx)=cos(x0)*cos(dx)-sin(dx)*sin(x0)
Diese Gleichung ist exakt, aber nuetzt uns zunaechst wenig, da wir uns auf diese Weise nicht der trigonometrischen Funktionen entledigen. Zunaechst bringen wir sin(x0) auf eine Form cos(x0). Es gilt :
sin(x0)^2+cos(x0)^2=1 => sin(x0)=Wurzel(1-cos(x0)^2)
=>
A)
cos(x0+dx)=cos(dx)*cos(x0)-sin(dx)*Wurzel(1-cos(x0)^2)
************************************************** ******
(Diskussion der Gleichung im naechsten Beitrag)
Wie wuerde man ueber eine differentielle Methode vorgehen ?
Einschub (kannst du ueberspringen)
Die Ausgangsgleichung waere :
dcos(x)/dx=-sin(x)=-Wurzel(1-cos(x)^2)
Das Differential ersetzt man durch eine Differenz. Deine Loesung ist formal 1.Ordnung, somit waere es einfach der Differenzenquotient :
[cos(x+k*dx)-cos(x)]/dx=-Wurzel(1-cos(x)^2)
Und folgender Schritt entspraeche einer numerischen Integration 1.Ordnung:
cos(x+k*dx)=cos(x)-Wurzel(1-cos(x)^2)*dx
/Einschub
Die Differenzengleichung wuerde lauten :
B) y(k+1)=C1*y(k)-C2*Wurzel(1-y(k)^2)
C1=1
C2=dy=2*Pi/N_abtast=m0 im Beispiel Pi/180
Die Gleichung B) lautet diskretisiert :
A) y(k+1)=C1*y(k)-C2*Wurzel(1-y(k)^2)
C1=cos(dx)
C2=sin(dx)
(Btw : Die Form hatte ich vor 20 Jahren zweidmensional implementiert nicht Euler Cromer)
Und deine Iteration lautet :
c) y(k+1)=C1*y(k)-C2*Wurzel(1-y(k)^2);
C1=1-m0^2/2;
C2=Wurzel(m0^2-m0^4/4);
(Ich habe hier y(k) gewaehlt um die Variable vom x der Ausgangsgkeichung zu unterscheiden)
Letzendlich sind alle Gleichungen formal erster Ordnung (nicht bezueglich der Fehlerordnung) und unterscheiden sich durch die "Integrationsmethode".
Die Additionstheorem Methode ist sogar exakt !
Ich meine dein Verfahren wird sich letztendlich als ein Praediktor Korrektor Verfahren erweisen. Von Heun zum Beispiel :
http://www.tm-aktuell.de/PDF/AWPTeil1.pdf
EDIT :
Deine Methode fuehrt eine Taylorapproximation der exakten Konstanten der Additionstheoreme durch. (siehe naechster Beitrag)
Heun koennte dennoch aehnliche Ergebnisse liefern.