Ist die Standardphysik einfacher als gedacht?

[Struktron]

Zitat von soon

Hallo Struktron,

da, wo die Naturkonstanten entstehen, gibt es die diskreten Objekte unserer Alltagsvorstellung noch nicht, - sag ich mal so.
Selbst die Glücklichen, für die die aktuelle Physik beinahe Alltagsvorstellung ist, haben von diesem Bereich der Natur bestenfalls den Hauch einer vagen Vorahnung.

Von daher verursacht es vermutlich bei einigen hier einen gewissen Widerwillen, dass du zuhauf technische und wissenschaftliche Begriffe benutzt, die deplatziert und nicht angemessen erscheinen, - selbst dann, wenn man es für möglich hält, dass an deinem Kram irgendetwas dran sein könnte.

Bei meinem "Kram" handelt es sich erst mal nur um einen explizit vorliegenden Algorithmus zur Beschreibung von 3 D Stößen harter Kugeln. Solche Stöße dann viele Millionen mal (mein heutiges .pdf und das zugehörige DeltaV.prn basieren auf 2.800 Durchläufen) ausrechnen zu lassen und dabei bewährte Wahrscheinlichkeitsverteilungen (Maxwell-Boltzmannsche Geschwindigkeitsverteilung) zu verwenden, ist nichts Neues. Neu ist vielleicht, dass das niemand bisher veröffentlicht hat.
Offensichtlich werden bei solchen Stößen Geschwindigkeitsbetragsdifferenzen verändert. Auch das ist nichts Neues.
Neu ist aber, dass die noch ungedeuteten Betragsveränderungen im Durchschnitt vieler Stöße gegen diese interessante Zahl streben.

Das Dilemma heutiger Erweiterungsversuche für die Standardphysik wird gut in "Hedrich, Reiner; Raumzeitkonzeptionen in der Quantengravitation (Spacetime in Quantum Gravity)" diskutiert. Das bestätigt dann die Diskussionwürdigkeit der alten Überlegungen für ein Substrat diskreter Objekte. Das Thema ist schwierig, wenn auch oberflächlich betrachtet meine Geschwindigkeitsübertragungen bei Berührung einfach erscheinen.

Zitat von soon

Bist du inzwischen dazu bereit, dir Ratschläge anzuhören, und auch darauf einzugehen?, - selbst auf die Gefahr hin, dass von deiner Physik nichts übrig bleibt?

Und ist dein Interesse an der Sache wirklich groß genug, so dass du auch den einen oder anderen kleinen Affront wegstecken kannst,: oder bist du immer noch dabei, nach einem preisgünsten Frack für die Nobelpreisverleihung Ausschau zu halten?

Auf ALLTOPIC wurde versucht, in diesem Sinn mit mir zu diskutieren. Leider nicht auf der Ebene der, einzelnen in Klartext und üblicher Nomenklatur vorliegenden, Algorithmen. Das ist vermutlich allen zu schwierig, auch hier. Freuen würde ich mich, wenn es auf diesem Weg gelingen würde, Spezialisten, welche schon mit Stößen unendlich harter Kugeln arbeiten, zu einer (nicht unbedingt öffentlichen) Diskussion zu überreden.

Viele Grüße
Lothar W.

[soon]

Hallo Struktron,

wenn man die Sache mittels einer Programmiersprache überprüfen will, wie wäre das Programm aufgebaut?

Man hat vermutlich einen Startwert, eine Berechnung und ein Ergebnis?


Startwert
Wie wird der Startwert bestimmt?

Berechnung
Die Berechnung interessiert mich bis auf weiteres nicht.

Ergebnis
Was geschieht mit dem Ergebnis?
Wird das Ergebnis zunächst nur abgespeichert oder wird es als Startwert wieder eingesetzt?



LG soon

[Struktron]

Hallo Soon,

Zitat von soon

,

wenn man die Sache mittels einer Programmiersprache überprüfen will, wie wäre das Programm aufgebaut?

Man hat vermutlich einen Startwert, eine Berechnung und ein Ergebnis?


Startwert
Wie wird der Startwert bestimmt?

Normal würde man bei einem realen Experiment, beispielsweise zum Billardstoß, eine Ebene auswählen, eine Kugel an einen Punkt der Ebene legen, die andere Kugel durch eine Vorrichtung auf eine bestimmte Geschwindigkeit in der Richtung auf die ruhende zu bringen und noch dazu versuchen, die ruhende in einem bestimmten Streifwinkel (an einer bestimmten Stelle) zu treffen. Das wären die Startwerte und das Ergebnis einer Messung würde die Winkel und Geschwindigkeitsbeträge nach dem Stoß festhalten.

Beim 3 D Stoß wäre das Experiment schwieriger durchzuführen. Haben wir nun aber Stoßtransformationen dafür, müssen diese auch für das zweidimensionale Experiment die richtigen Ergebnisse liefern. Für alle Anfangswerte mit einer ruhenden Kugel und einer mit beliebiger Geschwindigkeit bewegten. Nach oben gibt es in diesem nichtrelativistischen Fall keine Geschwindigkeitsbeschränkung. Und die zweite Kugel kann auch in Bewegung sein.

Da wir nun aber dreidimensionale Stöße betrachten, wo die Kugeln gleich schwer und unendlich hart sein sollen, wir aber die zu wählende Anfangsgeschwindigkeit (3 D Vektor) nicht kennen, können wir die bewährte Erfahrung verwenden, dass in jedem Gas harter Kugeln durch Thermalisierung die Maxwell-Boltzmannsche Geschwindigkeitsverteilung erzeugt wird. Mit der Inversionsmethode kann nun eine solche Geschwindigkeit zufällig gemäß der MB-Verteilung erzeugt werden.

In meinen Simulationen erzeuge ich im aktuellen Arbeitsblatt bei einem Durchlauf gleich zwei mal 1 Million solcher zufälligen Geschwindigkeitsvektoren. Das sind aber keine Startwerte für die weiteren Rechnungen, weil in meiner ortslosen Betrachtung jeder Stoß unabhängig von den anderen gerechnet wird.

Zitat von soon

Berechnung
Die Berechnung interessiert mich bis auf weiteres nicht.

Ergebnis
Was geschieht mit dem Ergebnis?
Wird das Ergebnis zunächst nur abgespeichert oder wird es als Startwert wieder eingesetzt?

Aus den Millionen Einzelergebnissen wird nur der Durchschnittswert der Geschwindigkeitsbetragsänderungen gespeichert.
In den nächsten Durchläufen gibt es vielfältige Möglichkeiten, diesen errechneten Durchschnittswert vom letzten Durchlauf zu verwenden:
- wird er gar nicht verwendet, läuft das auf eine Untersuchung im idealen Gas hinaus. Dabei interessieren die erzeugten Geschwindigkeiten und es kann überprüft werden, dass eine Thermalisierung erfolgt, welche die MB-Verteilung erzeugt
- wird er zur Veränderung einer der beiden MB-Verteilungen eingesetzt, ist das der stochastische Einfluss für den nächsten Durchlauf. Das ist meine aktuelle Vorgehensweise
- darüber hinaus gehende Einflüsse können richtungsabhängie Unterschiede der Anzahldichte (freien Weglänge) und der Geschwindigkeiten berücksichtigen. Dieses schwierigere Unterfangen wird hier noch nicht in Angriff genommen.

MfG
Lothar W.

[soon]

Hallo Struktron,

das ist zu viel Text als Antwort auf einfache Fragen. Mich interessiert nur der Programmablauf.

Du hast also Anfangswerte, die aus 3 Teilen bestehen, - davon hast du 1000000 Stück.
vektor : array[1..3] of double; ?
anfangswert : array [1..1000000] of vektor;

Das anfangswerte_array wird mittels random-Funktion mit Zahlenwerten gefüllt.
Die random-Funktion liefert entweder ganze Zahlen aus einem festzulegenden Intervall oder reelle Zahlen aus dem Intervall 0 bis 1 (0 <= X < 1).
Welche Werte sollen die Anfangswerte annehmen können?


Dann gibt es eine Schleife, in der mit jedem Element des anfangswerte_arrays eine Berechnung angestellt wird.
Die Ergebisse dieser Berechnungen werden in ein weiteres array geschrieben, um daraus einen Durchschnittswert ermitteln zu können.
Die Ergebniswerte sind wieder Vektoren?

ergebniswert : array [1..1000000] of vektor; ?

for n := 1 to 1000000 do
begin
Berechnung
Berechnung
ergebniswert[n] := Ergebnis der Berechnung;
end;

Dann: 'Durchschnittswert der Geschwindigkeitsbetragsänderungen'
Wie sieht diese Schleife - dem obigen Schema entsprechend - aus?

LG soon

[Struktron]

Zitat von soon

das ist zu viel Text als Antwort auf einfache Fragen. Mich interessiert nur der Programmablauf.

Dabei müssen wir aber in mein .pdf schauen:
Von (1) bis (18), also vor dem Abschnitt 4. sind alles Definitionen.
Mit (20) wird festgelegt, dass alle mit i indizierten Größen i mal berechnet und deren Ergebnisse intern gespeichert werden.

Zitat von soon

Du hast also Anfangswerte, die aus 3 Teilen bestehen, - davon hast du 1000000 Stück.
vektor : array[1..3] of double; ?
anfangswert : array [1..1000000] of vektor;

Das anfangswerte_array wird mittels random-Funktion mit Zahlenwerten gefüllt.
Die random-Funktion liefert entweder ganze Zahlen aus einem festzulegenden Intervall oder reelle Zahlen aus dem Intervall 0 bis 1 (0 <= X < 1).
Welche Werte sollen die Anfangswerte annehmen können?

Nicht aus drei Teilen, sondern bis (49) aus allen acht reellen Parametern, welche in die Stoßtransformationen (50) und (51) eingehen. Von deren Ergebnissen wird hier in dieser Simulation nur der Geschwindigkeitsbetrag benötigt. Mathcad macht das gleich in einem Schritt, ohne erst die Geschwindigkeitsvektoren hinschreiben zu müssen. Selbstverständlich lassen sich diese aber für andere Zwecke auch speichern. Dass verwendete Größen Zahlen, Vektoren oder Matrizen sein können, geht jeweils aus deren Definition hervor.

Die Werte, mit denen in (50) und (51) Stöße berechnet werden, sind keine Anfangswerte. Sie werden in (47), (48) und (49) errechnet. Dort werden die vorher errechneten Funktionswerte, welche zwischengespeichert wurden, aufgerufen. Man könnte alle solchen Funktionen in (50) und (51) einsetzen, was Mathcad sogar unterstützt. Mit den über eine Seite gehenden Formeln gewinnt man aber nichts. Falls sich diese sogar noch vereinfachen lassen, geht die Anschaulichkeit ganz und gar verloren.

Die zulässigen Werte werden durch die Form der Vektordarstellung festgelegt. Weil Kugelkoordinaten verwendet werden, kommen pro Geschwindigkeitsvektor zwei Winkel und ein Geschwindigkeitsbetrag vor. Deren Grenzen werden durch rnd() in links und rechts offenen Intervallen festgelegt. Echt reelle Zahlen gibt es allerdings genauso wenig wie echte Zufallszahlen.

Zitat von soon

Dann gibt es eine Schleife, in der mit jedem Element des anfangswerte_arrays eine Berechnung angestellt wird.
Die Ergebisse dieser Berechnungen werden in ein weiteres array geschrieben, um daraus einen Durchschnittswert ermitteln zu können.
Die Ergebniswerte sind wieder Vektoren?

ergebniswert : array [1..1000000] of vektor; ?

for n := 1 to 1000000 do
begin
Berechnung
Berechnung
ergebniswert[n] := Ergebnis der Berechnung;
end;

Dann: 'Durchschnittswert der Geschwindigkeitsbetragsänderungen'
Wie sieht diese Schleife - dem obigen Schema entsprechend - aus?

Man könnte das selbst auch so ähnlich programmieren. Deshalb noch mal die Vorgehensweise in meinem Arbeitsblatt:
Funktionen werden vor ihrem ersten Aufruf für eine Berechnung definiert. In Mathcad sind beim Funktionssymbol immer in Klammer die Variablen erforderlich. Das können aber auch Vektoren oder Matrizen sein.

In der eigentlichen Berechnung haben die Variablen einen Index i, welcher Millionen mal durchlaufen wird. Das erfolgt auch mit (50) und (51). Eine Besonderheit ist dann (52), wo die Änderung der Geschwindigkeitsbeträge definiert wird. Dieser Array, wie Du ihn wohl nennen würdest, enthält Millionen positive oder negative Zahlen. Deren Durchschnitt der Beträge wird in (53) berechnet. Nur diese Zahl wird geteilt durch 4 Pi in (55) an die Datei DeltaV.prn angehängt. Diese Datei kann von meiner Homepage herunter geladen werden.

Danach folgt nur die Auswertung.

MfG
Lothar W.

[soon]

Hallo Struktron,

ausser einem Verweis auf dein Arbeitsblatt, wiedermal, kann ich deiner Antwort nichts wirklich Konkretes entnehmen und bin raus.

LG soon

[Struktron]

Hallo alle miteinander,

jetzt gibt es eine neue Version meines Feinstrukturkonstante.pdf.

Es ist offensichtlich, dass Stöße gleicher Teilchen, im Idealfall vereinfacht in einem ortslosen HKG, durch einen Geschwindigkeitstausch parallel zu den Berührpunktnormalen (Stoßachsen), beschrieben werden können. Dabei gelten Energie- und Impulserhaltung. Bei der Simulation vieler solcher Stöße ergibt sich ein Geschwindigkeitsbetragsunterschied, dessen Durchschnittswert von ungefähr 0.0915401, beispielsweise auch durch ein in C geschriebenes Programm verifiziert wurde.
Unberücksichtigt ist in den klassischen Simulationen der Einfluss vorher in der Umgebung erfolgter Stöße. Diese können den Mittelwert der MB-Verteilung für Folgestöße verändern. Das wird in den Gleichungen (62) und (64) des neuen Feinstrukturkonstante.pdf ausgedrückt. Unklar ist aber bisher, wie die verwendeten Faktoren physikalisch nachvollziehbar neue Geschwindigkeitserwartungswerte für die nächsten Stöße erklären können. In der ortslosen Betrachtung sollten alle virtuellen Orte von vorhergehenden Stößen gleich berechtigt sein, aus deren Symmetrie unverschobene MB-Verteilungen für beide Stoßpartner folgen sollten.
- Bei der Thermalisierung werden aber bereits zwei unterschiedliche anfängliche Geschwindigkeitsverteilungen betrachtet. Daraus kann man schließen, dass eine zweite solche, also verschobene, MB-Verteilung nicht prinzipiell auszuschließen ist. Würde diese eine stabile Struktur in einer unterschiedlichen Umgebung beschreiben, könnten in dieser Menge ständig von der Umgebung im Durchschnitt abweichende Geschwindigkeitsbeträge erzeugt werden, ohne dass dabei der Energieerhaltungssatz verletzt wird.
- Es könnte aber auch sein, dass ohne ein notwendiges stabiles System, im normalen ortslos betrachteten HKG, durch sekundäre, tertiäre,... Stöße, welche vorher stattfanden, ein solcher Einfluss ausgeübt wird, welcher durch eine Reihe iterativ beschrieben werden könnte. In news:sci.physics.research gab es im thread "de vries formula for fine structure constant" neulich einen Hinweis:
"in 2004 hans de vries posted a terse, elegant and (still, to date)
accurate formula for the fine structure constant:

http://tinyurl.com/devriesconst

a formula in python2.7 would be as follows:

from math import pi,e

a = 0.007 # start off arbitrarily close to alpha
for x in range(1, 15):
t = 0.0
g = 0.0
for i in range(70):
g = g + pow(a, i)/pow(2*pi, t)
t = t + i
a = pow(g, 2)/(pow(e, (pow(pi, 2)/2)))
return 1/a

[update: when running this with 30 loops and using python
BigFloat (libmpfr) at 150 decimal places of precision
the following values are obtained:
137.03599909582961049584812391855684195959053299
0.007297352568653858214986442807070539674568087313 6
thus demonstrating that the algorithm is still within the
margin of error for at least the CODATA 2010 value of alpha]".

Das konnte ich noch nicht nachvollziehen, aber vielleicht führt es auf eine Formel, welche die Korrektur in meinem (64) durch den Einfluss der vorherigen Stöße mit einbezieht. De Vries definierte sein Gamma so:
"Gamma = 1 + alpha / (2 pi)^0 (1 + alpha / (2 pi)^1 (1 + alpha / (2 pi)^2 (1 +..."
sowie "alpha = Gamma^2 e^(-pi^2/2)"
und erhielt auch den exakten Wert gemäß CODATA.

Vielleicht schafft es hier jemand, diese Iteration zur exakten Erzeugung nach zu vollziehen. Mit einem guten Tipp könnte ich das dann ins Mathcad-Arbeitsblatt einbauen.
Viel Spaß und Erfolg bei den Versuchen,
mfG,
Lothar W.

[soon]

Zitat von Struktron

... neulich einen Hinweis:
"in 2004 hans de vries posted a terse, elegant and (still, to date)
accurate formula for the fine structure constant:

http://tinyurl.com/devriesconst

a formula in python2.7 would be as follows:

from math import pi,e

a = 0.007 # start off arbitrarily close to alpha
for x in range(1, 15):
t = 0.0
g = 0.0
for i in range(70):
g = g + pow(a, i)/pow(2*pi, t)
t = t + i
a = pow(g, 2)/(pow(e, (pow(pi, 2)/2)))
return 1/a

[update: when running this with 30 loops and using python
BigFloat (libmpfr) at 150 decimal places of precision
the following values are obtained:
137.03599909582961049584812391855684195959053299
0.007297352568653858214986442807070539674568087313 6
thus demonstrating that the algorithm is still within the
margin of error for at least the CODATA 2010 value of alpha]".

Wenn ich ein Spaßvogel wäre, würde ich auch soetwas versuchen:

Ich nehme eine Naturkonstante, bastel eine Iteration, iteriere, bis ich einen lustigen Wert bekomme, bezeichne diesen als mysteriösen Startwert und iteriere rückwärts. Wenn dann die Naturkonstante nicht wieder herauskommt, erzähle ich etwas von 150 Nachkommastellen, die ich brauche, so daß niemand den Quatsch nachprüfen mag.

- Ist nur eine Vermutung, da ich auf andere Werte kam, nachdem ich den Quelltext in Delphi eingetippt habe.

(procedure TForm1.Button1Click(Sender: TObject);
var
a,t,g,pi,e : extended;
x,i : integer;
begin
a := 0.007;
pi := 3.141592653589793238;
e := 2.718281828459045235;

for x := 1 to 15 do
begin
t := 0;
g := 0;

for i := 0 to 70 do
begin
g := g + power(a,i) / power(2*pi,t);
t := t + 1;
a := power(g,2) / (power(e,(power(pi,2)/2)));
end;
a := 1/a;

memo1.lines.add(floattostrF(a,fffixed,100,100));
end;

Ergebnis:
138,727507278841451000
138,727507278841451000
138,727507278841451000
138,727507278841451000
...


LG soon

[Struktron]

Hallo,

Zitat von soon

Wenn ich ein Spaßvogel wäre, würde ich auch soetwas versuchen:

Ich nehme eine Naturkonstante, bastel eine Iteration, iteriere, bis ich einen lustigen Wert bekomme, bezeichne diesen als mysteriösen Startwert und iteriere rückwärts. Wenn dann die Naturkonstante nicht wieder herauskommt, erzähle ich etwas von 150 Nachkommastellen, die ich brauche, so daß niemand den Quatsch nachprüfen mag.

- Ist nur eine Vermutung, da ich auf andere Werte kam, nachdem ich den Quelltext in Delphi eingetippt habe.

:
Ergebnis:
138,727507278841451000
138,727507278841451000
138,727507278841451000
138,727507278841451000
...

In Quanten.de hat "Herr Senf" ungefähr das gleiche Resultat 138,7 "zu Fuß" ermittelt.

Bei mir in Mathcad 14 (das leichter zum Spielen verwendet werden kann, als Mathcad Prime 2.0), ist das x von 0 bis 15 ganz ohne irgend einen Einfluss. Wie eine Iteration in Python oder Delfi erzeugt wird, weiß ich nicht. In Mathcad ergibt sich nach i > 7 keine Änderung mehr, aber etwas näher ist der Wert an dem der FSK: 0.00729722898866373 bzw. 137.03831982708817.

Ob die Behauptung des exakten FSK-Wertes aus news:sci.physics.research bzw. von De Vries nachvollziehbar ist, wissen wir noch nicht. Könnte denn die Rechengenauigkeit so einen Einfluss ausüben?

Unabhängig vom Ergebnis würde mich interessieren, ob man hinter den einzelnen Iterationsschritten oder hinter den Potenzreihen-Entwicklungen etwas Physikalisches erkennen kann? Könnte man nach meiner Monte-Carlo-Integration eine Fortführung durch eine konvergierenden Potenzreihe als Zusammenfassung vieler noch durchzuführender Simulationsschritte interpretieren?

MfG
Lothar W.

Nachtrag: Die ursprüngliche Formel von De Vries, in Mathcad so eingesetzt, dass mit beliebigem Wert begonnen wird, dann die Formel für Gamma maximal neun mal durchläuft und jedes mal der Wert alpha für den nächsten Durchlauf der Iteration verwendet wird, liefert am Ende 0.00729735256865386 ohne weitere Veränderungen bei weiteren Iterationen. Wichtig ist, dass mit verschiedenen Werten, also z.B. 0.06 oder 0.09,... begonnen werden kann.

[Struktron]

Hallo alle miteinander,

weil die Berechnung nach der einfachen Methode, wie eigentlich viele mathematische Konstante berechnet werden, hier von niemandem nachvollzogen wurde, habe ich selbst weitere Versuche dazu angestellt.

Mit Mathcad 14 ist es einfach: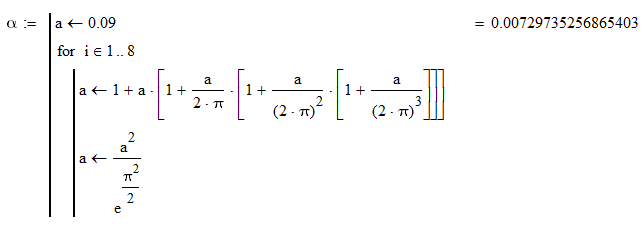


Weil es mit Delfi und Python scheinbar nicht funktioniert (Schande, dass hier niemand was davon versteht ), habe ich mir Python herunter geladen, komme aber nicht zurecht:


Dabei erfolgen zwar fünf Durchläufe der Iteration, aber a verändert sich nur ein mal.

In SMath ist die Rechengenauigkeit nicht ausreichend, es reicht nur für zwei Iterationen, dann kommt eine Fehlermeldung. Aber immerhin wird schon eine höhere Annäherung erreicht: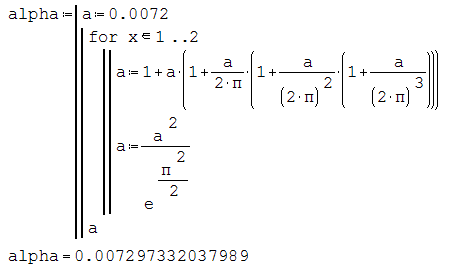


Das Grundprinzip für eine erfolgreiche Berechnung wird mit Mathcad Prime 2.0 deutlich: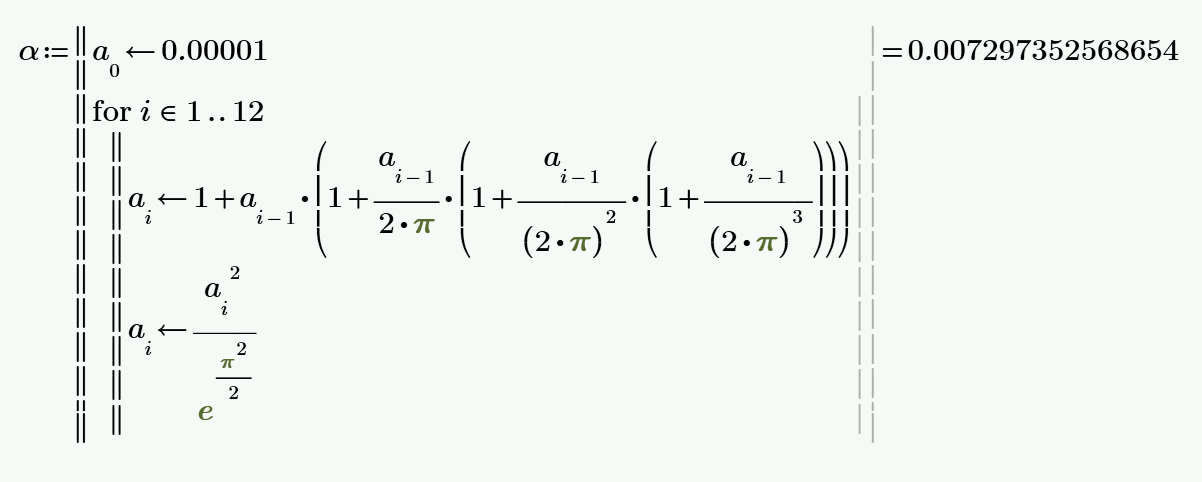


Für die Iteration sollten Vektoren verwendet werden, das Überschreiben alter Werte funktioniert nicht generell.

Zu sehen ist deutlich, dass die Feinstrukturkonstante demnach eigentlich als mathematische Konstante aufzufassen ist, weil sie wie andere solche Konstanten durch Reihenentwicklungen (=> auch Grenzwerte von Potenzreihen) mit hoher Genauigkeit errechnet werden kann. Eine physikalische Erklärung könnte auf Stöße zurück zu führen sein. Das öffnet viele neue Ansätze für Erklärungen in der Standardphysik.
MfG
Lothar W.