
 |
|
|||||||
| Quantenmechanik, Relativitätstheorie und der ganze Rest. Wenn Sie Themen diskutieren wollen, die mehr als Schulkenntnisse voraussetzen, sind Sie hier richtig. Keine Angst, ein Physikstudium ist nicht Voraussetzung, aber man sollte sich schon eingehender mit Physik beschäftigt haben. |
 |
|
|
Themen-Optionen | Ansicht |
|
#161
|
||||
|
||||
|
Zitat:
auch ein Feld existiert, das ein Teilchen mit der el.Ladung -Q beschreibt welches aber die selbe Ruhemasse wie das erste Teilchen besitzt! Das ist die erstmalige theoretische Berechnung/Vorhersage von Antimaterie, die direkt aus der ART folgt! Ausführlich nachzulesen in Einsteins Aufsatz "Elektron und Relativitätstheorie" erschienen 1925!, 3 Jahre vor Dirac seiner Deduktion von Antimaterie auf der Basis der SRT. Einstein zeigte, dass aus der Invarianz der diagonalen Metrik gegenüber Raumspieglung und Zeitumkehr auch die Invarianz der Masse gegenüber der Ladungskonjugation folgt. Die Teilchenmasse m muss daher für beide el.Ladungsvorzeichen dieselbe sein. m --> m für +Q --> -Q Da aber (1925) nur das Proton mit pos.el.Ladung und das Elektron mit neg.el.Ladung (die sich erheblich in der Masse unterscheiden) bekannt war, empfand Einstein seine aufgefundene Symmetrie als unerwünscht. Er zweifelte gar an seiner ART und stellte seine Arbeiten zur Einheitlichen Feldtheorie einige Jahre ein. Dirac dagegen, erklärte einfach die Protonen zu den Antiteilchen der Elektronen und führte dies in seinem Buch "Die Prinzipien der Quantenmechanik (1930)" expliziet aus. Diracs Überzeugung von der Richtigkeit der SRT und QM war so stark, dass er nicht bereit war den Widerspruch seiner Ergebnisse zur physikalischen Realität anzuerkennen. Diracs Annahme des Proton als Antielektron war unmöglich, weil die von Dirac verwendeten Symmetriegruppen verlangten, das Teilchen und Antiteilchen die selbe Ruhemasse besitzen und das jede Massedifferenz eine Brechung der SRT-Symmetrie der Raum-Zeit-Welt bedeuten würde. Dirac hatte aber Glück, da 1932 das Positron, das echte Antiteilchen des Elektron entdeckt wurde. Dies war das von EINSTEIN! (und eigentlich von Dirac auch) tatsächlich geforderte Elementarteilchen mit Elektronenmasse und pos.el.Ladung. Damit war nun auch für das Proton ein Antiproton mit der Masse des Protons vorauszusagen, was später auch entdeckt wurde. Somit wurde klar, das für JEDES Teilchen ein Antiteilchen existiert. Frohe Ostern EMI
__________________
Sollen sich auch alle schämen, die gedankenlos sich der Wunder der Wissenschaft und Technik bedienen, und nicht mehr davon geistig erfasst haben als die Kuh von der Botanik der Pflanzen, die sie mit Wohlbehagen frisst. |
|
#162
|
|||
|
|||
|
Hallo zusammen,
schönen Dank erst einmal für Eurer Feedback: Zitat:
Zitat:
 (Die beiden hellblauen "Dächer" / "3D-Dreiecke" über bzw. unter der Einheitsmatrix enthalten "im SRT-Fall" nur Nullen). Ge?ndert von SCR (03.04.10 um 08:55 Uhr) |
|
#163
|
|||
|
|||
|
Um ein wenig ein Gefühl zu bekommen einmal ein paar "ART-konforme" metrische Tensoren:
Metr. Tensor in der Schwarzschild-Metrik: 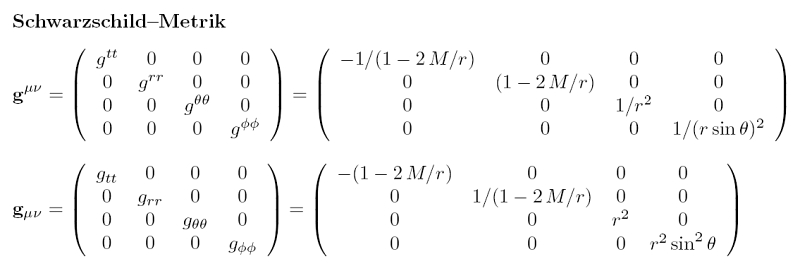 Zugehöriges Linienelement (mit G=c=1): 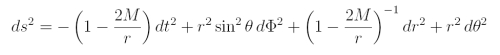 Metr. Tensor in der Kerr-Metrik: 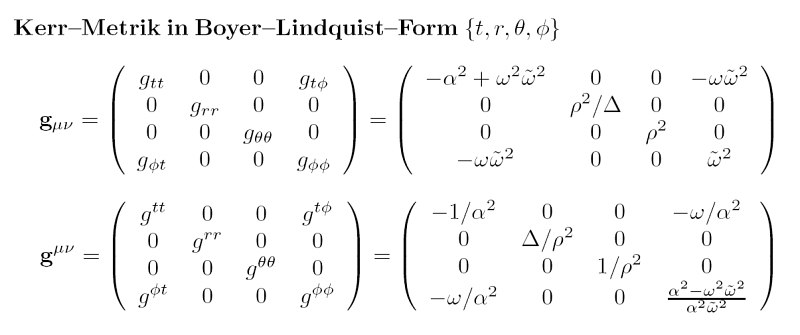 zugehöriges Linienelement (Boyer-Lindquist): 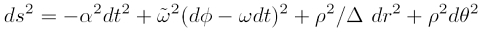
|
|
#164
|
|||
|
|||
|
Metr. Tensor in der Robertson-Walker-Metrik:
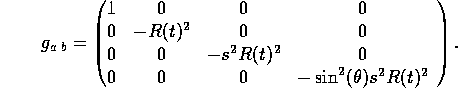 Zugehöriges Linienelement: 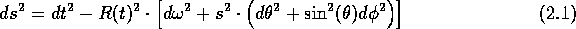
|
|
#165
|
|||
|
|||
|
Zitat:
Zitat:
 (In meinen Augen gar nicht einmal so abwägig - Aber das heißt ja nix (In meinen Augen gar nicht einmal so abwägig - Aber das heißt ja nix  .) .)Welche Form müsste ein "umfassender" Metrik-Tensor denn Deiner Meinung nach haben? |
|
#166
|
|||
|
|||
|
Zitat:
In der Tensorrechnung sind nämlich drei unterschiedliche Produkte denkbar: 1) Das skalare Produkt (U • V) zweier Tensoren m-ter und n-ter Stufe ist ein Tensor (m + n - 2)-ter Stufe. 2) Das vektorielle Produkt (U x V) zweier Tensoren m-ter und n-ter Stufe ist eine Tensor (m + n - 1)-ter Stufe. 3) Das tensorielle Produkt (U ¤ V) zweier Tensoren m-ter und n-ter Stufe ist ein Tensor (m + n)-ter Stufe; dazu sind alle Komponenten des ersten mit allen Komponenten des zweiten Tensors zu multiplizieren. Fazit: Der Anwender muss präzise wissen, welches Produkt er jeweils im Auge hat. Gr. zg Ge?ndert von zeitgenosse (03.04.10 um 20:02 Uhr) |
|
#167
|
|||
|
|||
|
Hi zg,
Zitat:
  ) )Am interessantesten finde ich im Moment den metrischen Tensor der Kerr-Lösung - wegen der Werte g14 (bzw. gΦt) und g41 (bzw. gtΦ); die Boyer-Lindquist-Koordinaten weisen allerdings Koordinaten-Singularitäten auf (z.B. bei g22 (bzw. grr) des oben dargestellten Metrik-Tensors: Δ -> 0) Die Kerr-Schild-Metrik umgeht diese Problematik:  Bei dieser Metrik ist aber im Vergleich zu Boyer-Lindquist die Zeitabhängigkeit jetzt weg. Oder ist die lediglich in den anderen Nebendiagonalen-Elementen "versteckt"?  Das muß ich mich einmal etwas näher ansehen (insbesondere g12, g21, g13 und g31) ... 
Ge?ndert von SCR (05.04.10 um 00:20 Uhr) |
|
#168
|
|||
|
|||
|
Zitat:
Durch das Raumwachstum bewegen sie sich (zunächst unmerklich) stetig beschleunigt voneinander weg. Auf Grund der relativen Bewegung zueinander wird ein dritter Beobachter (früher oder später) eine ZD zwischen beiden unterstellen: a) Wurden die Uhren überhaupt beschleunigt? b) Welche Uhr geht langsamer: A oder B? c) Woher stammt die E(kin)? ... Sind aber nur so ein paar Fragen "nebenbei" ... 
|
|
#169
|
|||
|
|||
|
Nächster Abschnitt der ART:
Zitat:
Ge?ndert von SCR (07.04.10 um 07:34 Uhr) |
|
#170
|
|||
|
|||
|
In Ergänzung:
(5) ausgeschrieben:  (5a) ausgeschrieben: 
|
 |
| Lesezeichen |
|
|