
 |
|
|||||||
| Quantenmechanik, Relativitätstheorie und der ganze Rest. Wenn Sie Themen diskutieren wollen, die mehr als Schulkenntnisse voraussetzen, sind Sie hier richtig. Keine Angst, ein Physikstudium ist nicht Voraussetzung, aber man sollte sich schon eingehender mit Physik beschäftigt haben. |
 |
|
|
Themen-Optionen | Ansicht |
|
#1
|
|||
|
|||
|
Hallo,
ich hoffe mal ich Spam das Forum nicht voll mit meinen Wissenslücken!  Nun gut, so weit ich weiß ist es ja so: Der Zustand eines Teilchens mit einem bestimmten Spinwert in einer bestimmten Raumrichtung ist zugleich nichts anderes als die Superpostion zweier gegensätzlicher Spinwerte in abweichender Raumrichtung. (Spin Up x ~ Spin Up/Down y oder Spin Up z ~ Spin Up/Down x) Woanders hat das mir jemand mal so beschrieben: Zitat:
Gilt das nun eigentlich so für alle Eigenschaften die ein QM-System haben kann? Wie wäre das z.B. beim Ort (x)? |
|
#2
|
|||
|
|||
|
Zitat:
Die Eigenfunktionen zum Ort (die "Orthonormalbasis") sind deshalb kein abzählbarer Satz von Basiszuständen sondern ein kontinuierliches Spektrum. In der Ortsdarstellung sind das die Deltafunktionen von Dirac. In der Ortsdarstellung (Koordinate x) wäre die Eigenwertgleichung einer Orts-Eigenfunktion Psi(x) zum Eigenwert x1 also x*Psi(x) = x1*Psi(x) x ist dabei eine Variable und x1 der feste Eigenwert. Die Funktion Psi(x) muss also offenbar überall verschwinden, aber bei x=x1 einen ganz scharfen Peak haben: eine Delta-"Funktion" delta(x-x1). Die allgemeine Lösung wäre dann nicht eine Summe über die gewichteten Basiszustände sondern ein gewichtetes Integral über diese Delta-"Funktionen" (wegen kontinuierlichem Spektrum) - die Anführungszeichen weil die Delta-"Funktion" streng genommen keine Funktion sondern ein Funktional ist. |
|
#3
|
|||
|
|||
|
Ist das nur beim Ort so?
|
|
#4
|
|||
|
|||
|
Nein, für Impuls liegt ebenfalls ein kontinuierliches Spektrum vor.
Bei Energien mischt es sich: für gebundene Zustände liegt ein diskretes Spektrum vor (z.B. Atom-Orbitale); ist die Energie des Quants aber oberhalb der Potentialschwelle, so ist das Energiespektrum kontinuierlich. Man sieht das recht anschaulich beim Energiespektrum des Wasserstoffatoms, wie die Niveaus immer enger zusammenrücken, wenn man sich "von unten" der Ionisationsenergie nähert: 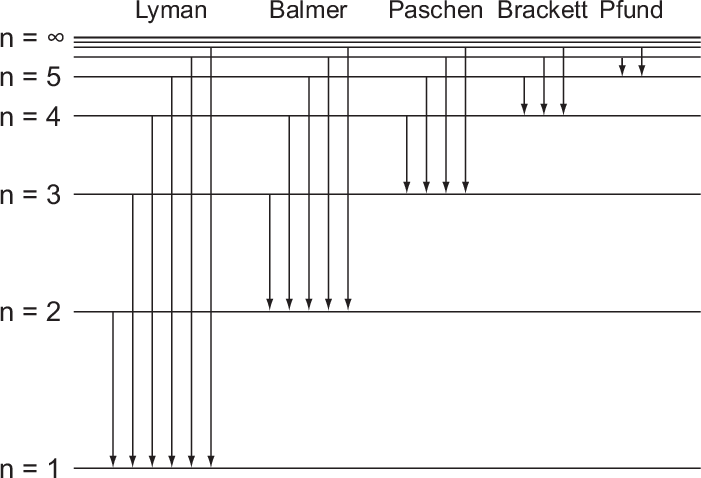 Die Eigenwerte von Drehimpulsen sind immer diskret. |
|
#5
|
|||
|
|||
|
https://phys.org/news/2016-06-physic...um-limits.html
Was in dem Artikel steht müsste doch auch für ein einzelnes Silber-Atom z.B. bei Stern-Gerlach gelten. Ich versuch das mal mit meinem Halbwissen anzuschneiden! Wenn ich ein Silberatom habe und es hat irgendeine Superpostion und dann kommt der 1. Magnet und es findet eine Messung statt, dann werden doch die entsprechenden Vektoren im Hilbertraum gedreht. Ich messe Up oder Down z.b. mit 50/50. Dauert dieser Vorgang Zeit, genau diese Drehung der Vektoren? Und wie wäre das dann beim Zeitentwicklungsoperator? (Der ja auch so eine "Drehung" bewirkt.) Vielleicht kann da jemand genau darauf eingehen, welcher Vorgang bei so einem Ablauf, ein Teilchen in Superpostion wird gemessen, denn genau Zeit braucht. Bzw. welcher Teil keine Zeit braucht. Ich dachte immer so dunkel, wenn ich irgendwelche Vektoren im Hilbertraum durch einen Operator verändere, dass dies dann keine Zeit braucht. Weil ja jegliche (unitäre) Zeit(entwicklung) selbst nur durch den Zeitentwicklungsoperator "vorgegeben" ist. Zitat:
THX schonmal vorab. 
|
|
#6
|
|||
|
|||
|
Nochmal nen Nachtrag zum Vorpost etwas anders:
Zitat:
Hat das grundsätzlich speziell etwas mit den "Dichtematrizen" bzw. der "Dichtematrix" zu tun, die es in der QM gibt? BTW: Ich habe etwas gefunden beim kurz Suchen: aber mehr als die "Überschrift" habe ich davon nicht gelesen. Verlinke das trotzdem mal --> Quantum mechanics in metric space: wave functions and their densities https://arxiv.org/abs/1102.2329 |
|
#7
|
|||
|
|||
|
Ich versuche mal als Laie einige Fragen zu beantworten und hoffe keine Fehler zu machen.
Zitat:
(Interessanter Artikel ist bei Wikipedia: https://de.wikipedia.org/wiki/Quante...nische_Messung) Zitat:
Wenn wir bspw. den Impulsoperator nehmen, so ist er im Ortsraum -ihquer*d/dx und eine Ableitung benötigt ja in dem Sinne keine Zeit. Auch bei einem formalen Zustandswechsel des Systems, wie c†|0>=|1> mit c† als Erzeugendenoperator spielt die Zeit keine Rolle. Zitat:
Ich kenne die Dichtematrix nur zur Beschreibung von Polarisation von Elektronen-Zuständen.
__________________
www.quantenforum.de |
|
#8
|
|||
|
|||
|
Dankeschön!
 Das hilft mir weiter. Das hilft mir weiter.Zitat:
Zitat:
Zitat:
|
 |
| Lesezeichen |
|
|