
 |
|
|||||||
| Registrieren | Hilfe | Benutzerliste | Interessengemeinschaften | Kalender | Suchen | Heutige Beitr?ge | Alle Foren als gelesen markieren |
| Quantenmechanik, Relativitätstheorie und der ganze Rest. Wenn Sie Themen diskutieren wollen, die mehr als Schulkenntnisse voraussetzen, sind Sie hier richtig. Keine Angst, ein Physikstudium ist nicht Voraussetzung, aber man sollte sich schon eingehender mit Physik beschäftigt haben. |
 |
|
|
Themen-Optionen | Ansicht |
|
#1
|
|||
|
|||
|
Folgende Situation:
Bob sitzt im Raumschiff un sieht auf seiner y-Achse einen Ball mit 10 m/s zwischen zwei Spiegeln im Abstand von 5m hin- und herpendeln, d.h. seine Uhr hat eine Frequenz von 1Hz. Nun sieht Alice Bob's Raumschiff mit 0,9c auf der x-Achse dahinfliegen. Dieser Sachverhalt ist eigentlich recht anschaulich darstellbar im Minkowski-Diagramm. Dabei werden die Winkel z.B. zwischen ct und ct' berechnet nach 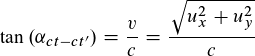 Das heißt die Zeitdilatation ergibt sich aus dem Gesamtgeschwindigkeitsvektor (auch wenn man hier die 10m/s vernachlässigen könnte). Stimmt das so? Meine nächste Frage: Wie werden die Winkel der einzelnen Raumdimensionen gedreht? Hängen die nur ab von der Geschwindigkeitskomponente des beobachtenen System bezogen auf die entsprechende Raumdimension? Das müsste meines Erachtens ja so sein denn die y-Komponenten im ensprechenden Beipiel sind ja y = y'. Mein Fazit wäre daher das der Betrag des Winkels zwischen ct und ct' = der Summe der Winkel der Raumdimensionen ist. Also fürs 4D-Diagramm: 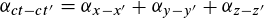 was sich ja eigentlich schon logisch ergibt wenn man bedenkt das 4D Linienelement invariant sein unter der LT muss. DIe Frage kommt auf, weil ich nun viele Bücher durchgegangen bin und das Minkowski-Diagramm meist nur in 2D erklärt wird. Dann wird immer davon ausgegangen das die Winkel zwischen ct und ct' sowie x und x' gleichgroß sind was aber meines Erachtens nicht gelten muss für Projekionen auf eine Achse in einem 3D Diagramm. Für ein 3D Diagramm werden dann aber keine Winkelberechnungen angegeben. Um auf das Eingührungsbeipiel zurückzukommen, war meine Idee den Schnitt der ct und y Achse darzustellen wobei dann ct' gedreht ist y' aber nicht. Das würde helfen zu verstehen warum man eine Zeitdilatation in y-Richtung hat aber keine Längenkontraktion. Mittlerweile bin ich mir aber nicht mehr sicher ob das so richtig ist. |
|
#2
|
|||
|
|||
|
Hallo mojorisin,
Zitat:
Bobs Weltlinie startet dann im Ursprung des Minkowski-Diagramms und läuft genau parallel zur t-Achse. Die Weltlinie des Balls startet im gleichen Punkt wie Bobs Weltlinie, bildet aber eine Sägezahnlinie entlang der t-Achse. Der y-Wert nimmt dabei periodisch zu und wieder ab. Ferner sieht Bob Alices Raumschiff mit 0,9c auf der x-Achse dahinfliegen. Das gestrichene Alice-System hat damit eine gekippte t'- und x'-Achse. Der Winkel zwischen der t und der t'-Achse ist gleich alpha. Der Winkel zwischen der x und der x'-Achse ist ebenfalls gleich alpha. alpha kennst Du, weil Du die korrekte Formel dazu angegeben hast. Jetzt kann man Ereignisse auf der Weltlinie des Balls in das Alice-System übertragen. Dass der Ball in y-Richtung hüpft macht die Sache natürlich nicht einfacher. Du könntest also zur Übung vorab den Ball erst mal in x-Richtung hüpfen lassen und dann geeignete Ereignisse auf dieser Weltlinie in das Alice-System übertragen, um zu testen, ob Du mit Minkowski-Diagrammen korrekt rechnen kannst. Wenn das klappt, kannst Du den Ball auch in y-Richtung hüpfen lassen. EDIT: Die y'-Achse ist parallel zur y-Achse. Die z'-Achse ist parallel zur z-Achse. Da Bob genaugenommen eine Uhr betrachtet, sollte es egal sein, in welche Richtung der Ball hüpft. Alice sollte immer den gleichen Dilatationsfaktor messen. Um den Dilatationsfaktor auszurechnen muss man zwei eindeutig definierte Ereignisse auf der t-Achse in das System von Alice transformieren.
__________________
Freundliche Grüße, B. Ge?ndert von Bernhard (24.08.17 um 21:33 Uhr) |
|
#3
|
|||
|
|||
|
Die X-Achse ist, räumlich gesehen, auch deckungsgleich mit der X'-Achse. Der "Winkel" zwischen X und X' ist in Zeitrichtung!
|
|
#4
|
|||
|
|||
|
Hallo Bernhard und Ich,
Danke für eure Antworten. Ich denke mein Problem lag darin dass ich versucht habe die ct'-y'-Ebene auf die ct-y-Ebene abbzubilden und das nicht richtig hinbekommen habe. Dabei war mir nicht klar wie sich die ct'-Achse darstellen lässt da sie ja eigentlich in den "Raum" hineingekippt ist. Aber ich denke ich habs jetzt verstanden. Das invariante Linienelement ergibt sich ja aus der Diagonalen des entsprechenden Elements. D.h. im 2D Diagramm aus der Diagnolen eines Quadrats im Ruhesystem bzw. eines Parallelogramms im relativ bewegten System wie im unteren Bild:  Erweiteret man das Diagramm zum 3D Diagram erhält man das Linienelement als Diagonale im enstrechenden Würfel (Ruhesystem) oder im entsprechenden Parallelepiped im relativ bewegten System 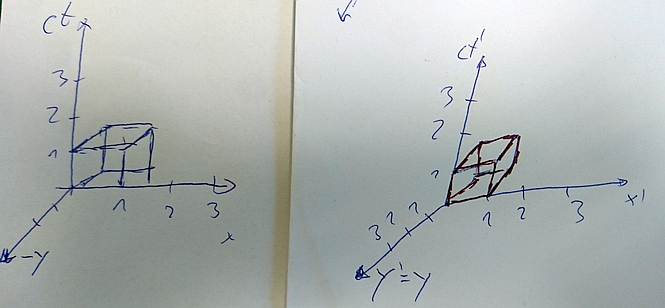 In EIngangspost beschrieben Fall ist die y'-Achse senkrecht zur ct' Achse da die Geschwindigkeit nur 10 m/s beträgt während die ct'-Achse und die x'-Achse einen Winkel <90° einschließen. Man könnte jetzt hier die Abbildung machen von der ct'-y'-Fläche auf die ct-y-Fläche und würde sehen das wie erwartet Abstände von ct'>ct sind ist wobei y' = y ist. |
|
#5
|
|||
|
|||
|
Das heißt meine eigentliche Hauptfrage wäre noch ürbig:
Sind folgende Formeln zur Berechnung der Winkel in einem 4D-Minkowskidiagramm richtig? Berechnung der ct-Achse: 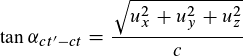 Berechnung der x-Achse: 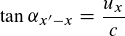 Berechnung der y-Achse: 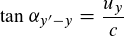 Berechnung der z-Achse: 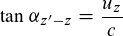
|
|
#6
|
|||
|
|||
|
Zitat:
 Wenn Du einen Boost in eine vorgebbare Richtung betrachten willst wird die Sache relativ kompliziert. Die zugehörige Lorentz-Transformation besteht dann aus einer räumlichen Drehung und einem Boost in die x-Richtung. Mit Hilfe dieser zusammengesetzten Transformation könnte man die Basisvektoren des gestrichenen Systems berechnen und daraus dann die Winkel zwischen den Achsen, allerdings wird das dann vergleichsweise unanschaulich. Wenn Du bei dem einfachen Boost in x-Richtung bleibst, so hat die x'-Achse im 2D-Minkoswki-Diagramm (mit der x- und der t-Achse) die Steigung v/c und die t'-Achse die Steigung c/v. Meine Empfehlung wäre es bei diesem Boost zu bleiben und damit zu rechnen.
__________________
Freundliche Grüße, B. |
|
#7
|
|||
|
|||
|
Zitat:
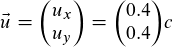 Mir ist klar, dass ich in dem Fall, das Koordinatensystem auch in die Richtung des Geschwindigkeitsvektors legen kann und dann ein 2D-Diagramm daraus machen mit u = 0,56 c Mir geht es aber darum ein Verständnis dafür zu bekommen wie man höherdimensionale Minkowski-Diagramme erstellen kann, für Fälle in denen man keine Reduzierung auf 2D mehr machen kann. |
|
#8
|
|||
|
|||
|
Im Beispiel siehst du ja schon, dass die ux und uy-Steigungen 0,28 sein müssen und nicht 0,4. Ich muss bloß zugeben, dass ies mir gerade zu anstrengend ist, die korrekte Formel herzuleiten. Vielleicht hast du selbst eine Idee (es handelt sich um einen Gradienten in einem rotierten Koordinatensystem).
|
|
#9
|
|||
|
|||
|
Zitat:
Damit kennt man die Lage aller vier Achsen des gestrichenen Systems in Bezug auf das ungestrichene System.
__________________
Freundliche Grüße, B. Ge?ndert von Bernhard (26.08.17 um 10:52 Uhr) Grund: Nicht weiter zitierte Formulierung geschönt. |
|
#10
|
|||
|
|||
|
Danke euch beiden,
Mit dem Zitat:
Zitat:
|
 |
| Lesezeichen |
| Themen-Optionen | |
| Ansicht | |
|
|